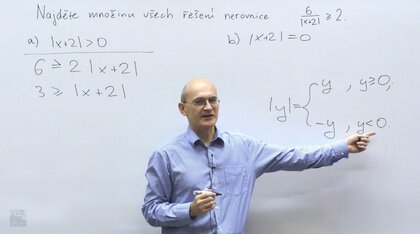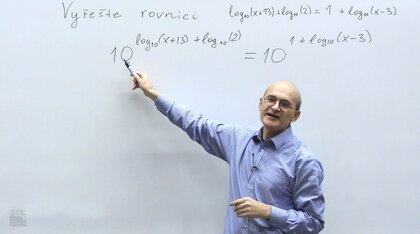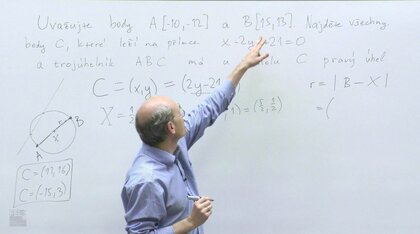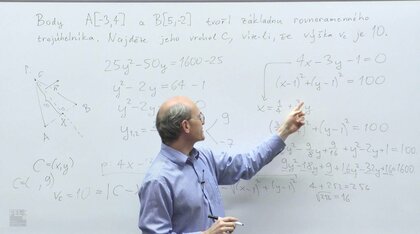V tomto seriálu se podíváme na témata, která se pravidelně objevují v přijímacích zkouškách na ČVUT FEL a která zároveň překvapivě často trápí (některé) studenty v prvním semestru, zejména v matematické analýze. Nebude to nějaký ucelený výklad látky. Učení matematiky totiž obvykle zahrnuje dvě fáze. Nejprve je třeba se některé věci naučit nazpaměť (typicky vzorce nebo třeba algoritmy). S tím vám stejně nepomůžu, to se musíte naučit sami, takže nějaké seznamy vzorců tady nečekejte, spíš občas připomeneme, co je třeba se naučit.
Nás bude zajímat zejména druhá fáze, ve které se člověk učí používat to, co už umí. Jinak řečeno, předpokládá se, že divák už ledacos ví, a cílem je podívat se na tyto znalosti z pohledu člověka, který chce řešit určité typy problémů. Znalosti se přitom uspořádají, třeba i začnou dávat smysl, ukážeme si také typické motivace a přístupy. Možná také některé věci uvidíte trochu jinak než ve škole, což je určitě užitečné.
Hodně trpělivosti přeje pH.
Videokurz si můžete pustit i jako playlist přímo na YouTube.
Vedle tohoto video kurzu doc. Habala připravil sedmero pozastavení nad všedně-nevšedními problémy s názvem „Humorná matematika“.